Unprojections Explained

Recently, one of the responses to the Reconstruction Positions […] post dealt with the unprojection of frustum corners. More specifically: with the inverted projection matrix and the final division with the $w$ coordinate. Being the lazy sod that I am on Sundays, I thought I’d quickly google it and paste a link with the explanation. Only one problem: I couldn’t find any decent articles! At least not within a reasonable amount of time, that is. I’m sure they’re out there somewhere ;) Most people asking “How do I unproject?” or “How can I get view space positions from a screen/mouse position?”* were told to check out existing open source code and copy it. That would indeed solve the issue at hand, but if you’re anything like me, you don’t like using code you don’t truly understand. So here’s my attempt to explain (Also… Mathematical rigour? What’s that? :) ).

*This question is also addressed in the earlier mentioned posts, but they’re geared toward shader-based post-processing, and it skimps over the unprojection part.

Homogeneous coordinates

In order to understand “un”-projections, it would help to know how projections work in the first place. I’ll probably be a bit too verbose in this part, but I reckon it’s good to have a proper intuitive grasp on it.

When working in regular 3D space, we tend to use 4D coordinates to differentiate between vectors and points (by setting the fourth – $w$ – coordinate to 0 or 1, respectively). This lets us use 4D matrices to perform affine transformations (for example: rotations, scale, and translations and combinations) with a single matrix, without having translations affect vectors (since $w$ == 0, the translation component will be nullified). If you’re not rolling your eyes at this point because I’m stating the obvious, you should grab any book on 3D programming math and revise :)

Anyway, these 4D coordinates are called homogeneous coordinates. Before projecting, the homogeneous aspect doesn’t really matter because the $w$ coordinate is hardly used. But, since we’re operating in 4D, we can do things not possible with a simple matrix in 3D, including projections. Projections are extensively covered all over the place, but let’s revisit homogeneous coordinates and how they’re relevant for this article.

More generally, homogeneous coordinates can be seen as an “extension” to regular $(x,y,z)$ triplets by adding said $w$ coordinate, moving towards 4D. They map back to good old 3D as follows:

$(x', y', z') = (\frac{x}{w}, \frac{y}{w}, \frac{z}{w})$

This is a projection from 4D to 3D. This is in fact also used to “rearrange” the z coordinate for perspective projections to get the divide-by-z, but you can find that explained in any proper 3D book as well. You’ll see that any scalar multiple of homogeneous coordinates will project to the same 3D point. For example, a point $\lambda (x, y, z, w) = (\lambda x, \lambda y, \lambda z, \lambda w)$

$(\frac{\lambda x}{\lambda w}, \frac{\lambda y}{\lambda w}, \frac{\lambda z}{\lambda w}) = (\frac{x}{w}, \frac{y}{w}, \frac{z}{w}) = (x', y', z')$

So, we see that a homogeneous point $\textbf{p}$ and $\lambda \textbf{p}$ represent the same 3D point, and we call scalar multiples of homogeneous points equivalent:

$(x, y, z, w) \equiv \lambda (x, y, z, w)$

We’re used to work with the subset where $w = 1$ . I’m not sure if there’s an actual name for this set, but let’s call them the principal representation of the point to make things easier to explain (that’s right, I’m coining things here!). This is almost always the representation we want in the end.

A final note about when $w = 0$ . These points are called ideal points, and have some practical applications which we don’t need to concern ourselves about here. Multiplied with a scalar, an ideal point remains an ideal point. Furthermore, they are projected at infinity (division by 0). They don’t correspond to proper 3D points, which is at the base of why we can use them to represent vectors. But since we’re just dealing with points from now on, let’s let it rest at that :)

Check your 3D math books chapter again on (perspective) projection, and you should have a better idea of how the homogeneous coordinates function theoretically beyond “divide by $w$ for perspective foreshortening”. In any case, the important part here is this: scalar multiples of homogeneous coordinates represent the same 3D point.

Unprojecting

Your usual every day projection happens as follows:

Provide a point in view space (principal representation, $w = 1$ ).
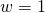Multiply with the projection matrix: this yields a homogeneous coordinate with non-principal representation.
Divide by 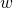$w$ to get the projected point in principal representation (the GPU does this for you for the vertex shader’s position output). This yields normalized device coordinates (NDC).

$\textbf{p}_{hom} = M \textbf{p}_{view}$

$\textbf{p}_{ndc} = \frac{\textbf{p}_{hom}}{w_{hom}}$

So when “unprojecting”, we want to figure out $\textbf{p}_{view}$ when we know $\textbf{p}_{ndc}$ *. Simple solving, right?

* You may not know the full NDC coordinates and only window $(x, y)$ coordinates, but that’s okay, see below.

$\textbf{p}_{hom} = \textbf{p}_{ndc} w_{hom}$

$\textbf{p}_{view} = M^{-1} \textbf{p}_{hom}$

But wait, you’d need to know $w_{hom}$ to calculate $\textbf{p}_{hom}$ ! Mission impossible, because that’s obviously part of what we’re trying to figure out! But remember, we’re dealing with homogeneous coordinates here, so we can use the equivalence property. $w_{hom}$ is a simple scalar, which means $\textbf{p}_{hom}$ and $\textbf{p}_{ndc}$ are equivalent; they represent the same point! The matrix transformation does not affect equivalence, which means:

$\textbf{p}_{homogeneousView} = M^{-1} \textbf{p}_{ndc}$

is a homogeneous coordinate equivalent to $\textbf{p}_{view}$ . The last thing to do is map that back to the principal representation and we have the correct result:

$\textbf{p}_{view} = \frac{\textbf{p}_{homogeneousView}}{w_{homogeneousView}}$

To recap, unprojection happens as follows:

Provide an NDC coordinate.
Multiply with the inverse projection matrix, yielding a homogeneous coordinate equivalent to the view position.
Divide by 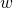$w$ to get the principal representation of the view position.

This should at least explain what’s going on in the position reconstruction post. The coordinates unprojected there are the NDC coordinates corresponding to the frustum corners.

What about screen positions?

If all you have are coordinates on the screen such as a mouse position, there’s some info lacking, huh? NDC coordinates are 3D so we’re obviously missing a $z$ component. But first things first, let’s give you the NDC $x$ and $y$ components. They’re obtained by a simple remapping to a [-1, 1] range:

$(x_{ndc}, y_{ndc}, z_{ndc}) = (2 \frac{x_{screen}}{width_{screen}} - 1, 2 \frac{y_{screen}}{height_{screen}} - 1, ???)$

But $z_{ndc}$ is an unknown. This shouldn’t be surprising, as a whole ray of points in space project to that same point on the screen. You’re essentially free to pick your own $z$ coordinate and something along that ray will come up. A value of 1 represents the intersection of the ray with the camera’s far plane. A value of 0 (DirectX) or -1 (OpenGL) represents one on the near field. You can use either to get an unprojected position and together with the camera position in the same space, this can be used to construct a ray to perform ray intersection tests in your scene.

I hope this helped if you’re struggling to figure out this stuff. Until next time!

Der Schmale – Real-time 3D programming

David Lenaerts – Freelance graphics programmer

Homogeneous coordinates

Unprojecting

What about screen positions?

Leave a Reply

Homogeneous coordinates

Unprojecting

What about screen positions?

Related posts

Leave a Reply